A Course in Modern Abstract Algebra, post 001

In Fall 2017, I taught Modern Algebra (aka “Abstract Algebra”) for the first time in many years.  For the next time I teach this class, I am considering putting here a version of my notes, instead of just distributing them in class.  Whether I do or not, I am providing here now a kind of “Learning Algorithm” or “Study Algorithm”, or as you may call it, a set of “Study Guidelines”, for every class you take, especially problem solving oriented classes, like this Modern Abstract Algebra class.

The overall plan is to use a textbook, but also I will use notes from when I took the course, augmented with things I’ve learned since then, and augmented with my thoughts on the textbook.  In Fall 2017, I used the text by Pinter (see Pinter’s Abstract Algebra Book), which is the same text that was used by my predecessor for quite a few years.

Here are some general study, learning, and course-taking recommendations:

1. Plan to read the textbook more than once, and then execute that plan, for instance, according to the remainder (see steps 2, 3, … below) of this algorithm.
2. Learn any suggested software (e.g. PROLOG, MathCAD, Maple, UACalc, Mathematica, MatLAB, Fortran, C++, LaTeX, Mathematica, Wolfram Alpha, etc), or online systems (e.g. Quora, StackExchange, Proceedings of the American Mathematical Society, Instructure Canvas, MyMathLab, GAP, Par GP, etc) to assist your learning of the material.
3. On the first reading of the textbook, give the problems only a cursory glance.  “Read it like a novel.”
4. Ask your classmates questions that you have about the reading.  Take notes about their answers.  Keep these notes organized.  When asking or answering questions, treat your classmates with the same respect that you think you deserve.
5. Participate in class and take notes during every class meeting.  Keep your daily notes organized.  Respectfully ask questions about the class lectures.
6. Form a study group (not a homework solution group).  Discuss within your study group your daily notes and the notes you take of the answers given by your classmates about the reading, and the questions that they pose to you, and your answers to their questions.  When asking or answering questions, treat your study group colleagues with the same respect that you think you deserve.
7. Later (see below), when working (unassigned or assigned) problems, use a fresh page for each problem (or type your solutions using a mathematics friendly document preparation system like LaTeX or LyX, which allows you to insert space as needed).
8. Prepare to write your solutions to problems, and to write your course notes, in complete sentences, using “English with Embedded Mathematics”.
9. On the second reading, solve on your own the first problem from each section of the textbook, long before any homework is assigned by your instructor.  File your solutions, so that if they are assigned later, you have them ready for proofreading, editing, correction, and submission.
10. Ask your questions about the reading in class or in an online forum as indicated by your instructor.  Repeat as instructed or as invited.
11. Anytime in this process of reading, learning, and participating in class, when you are assigned problems to turn in, go through your files of problems you already worked, and edit out any errors, and then submit the corrected solutions, but solve all other assigned problems as instructed also; then continue this “learning algorithm” on your own pace.
12. Visit your instructor during office hours to ask questions about the reading, and about the notes you took in class.  Take notes in these office hour meetings, and file your notes for later use.  Use them to help revise misunderstandings that you have developed during the course.
13. Anytime in this process, if someone provides you a solution to a problem that you should do on your own, make a note of that fact when you write your own version of the solution.  If the problem is assigned to turn in, cite your source (in fact, for your further understanding of the subject, it will usually be helpful to cite the sources in your filed problems, even for problems not to be submitted), and ask the instructor if you should do an extra problem, to compensate for the fact that you did not actually solve that problem on your own.  In fact, attempt to make up a new related problem (hopefully of similar difficulty to you) yourself, and solve that problem, and explain why you are doing this.
14. When graded work is returned, rework any problems for which your attempted solutions were incorrect, and take notes about your errors (keep the erroneous work as well as the correct work, so that you can remind yourself not to make the same errors later).
15. With instructor approval (because your instructor may allow you to resubmit solutions, and may require that you do this revision work on your own as well), discuss in your study group the solutions to problems that have been graded.
16. On your third reading of the textbook, solve on your own the second and third problems from each section of the textbook.
17. Continue to meet with your study group to learn more.  If exams are part of the graded component of the course, practice problem-solving potential exam questions in your study group.  Keep notes about any errors or correct solution methods or correct problem solutions.
18. Determine which sections you feel you understand well.  In all subsequent readings, skip these sections, and only solve the associated problems (on your own).  Continue to do this planning and task list revision after each subsequent reading of the textbook.
19. On your fourth reading (of the sections that you still feel you need to read), solve (on your own) the fourth, fifth, and sixth problems of each section.
20. Continue to meet with your study group to learn more.  If project proposals, projects, or project reports are part of the graded component of the course, brainstorm in your study group about possible project ideas and how to write proposals or reports.  Keep notes about any errors or correct writing methods or correct document preparation methods, etc.  Plan to not do a project on the same topic as any of your classmates, unless expected by your instructor.
21. Visit your instructor during office hours to ask questions about the reading, and about the notes you took in class, and, if project proposals, projects, or project reports are part of the graded component of the course, discuss the appropriateness of potential topics for your assignment.  Take notes in these office hour meetings, and file your notes for later use.  Use them to help guide you in your preparation for that assignment.
22. On your fifth reading, solve (on your own) all remaining problems in each section.
23. Continue to meet with your study group to learn more.  If presentations (in person or on video) are part of the graded component of the course, discuss in your study group about possible presentation ideas and perhaps how to script and video record your presentations, as well as how to upload or submit them.  Keep notes about any technical questions or issues that arise.    Plan to not do a project on the same topic as any of your classmates, unless expected by your instructor.
24. Visit your instructor during office hours to ask questions about the reading, and about the notes you took in class, and, if presentations (in person or on video) are part of the graded component of the course, discuss the appropriateness of potential topics for your assignment, and discuss any technical questions or issues that arose for your study group in understanding how to present or video record or upload/submit your presentations.  Take notes in these office hour meetings, and file your notes for later use.  Use them to help guide you and your group in your preparation for that assignment.
25. Enjoy learning!!

 

 

 

 

 

 

 

Book Recommendations

1.  I recall reading about Waldos in high school in the 1970s.  Specifically, I have been for most of my life an avid fan of science fiction and science fact, and I read about Waldos in a science fiction story.  You can read the original story by Robert Heinlein here:  
2. For years, I have used the text Models and Ultraproducts:  An Introduction, along with several others, to teach logic.  You can access it on the internet archive:  

I will add other recommendations later.

Differentiability Implies Continuity ~~ A Response to Part of Timothy Gowers post on the Cambridge Mathematical Tripos

Professor Timothy Gowers, of Cambridge University Department of Pure Mathematics and Mathematical Statistics, has posted some thoughts about the Cambridge Mathematical Tripos. He shows some model answers, and in his discussion of the “easy” part of the examination, he indicates that for students taking the tests, speed can be an over-riding concern. In one instance, Professor Gowers presents model answers to the problem of showing that for a real-valued function, differentiability implies continuity. I will propose a briefer, more intuitive, model answer for students who are interested in speeding up their progress through many parts of such a test. Here I shall give only four such examples from the Robinson/Zakon/Luxemburg, etc school of nonstandard analysis, each of which is a reasonable model answer to the same question, namely, “Show that for a function of one real variable, differentiability implies continuity.”

Model Answer 1:

Since f is differentiable, if , then . Since the product of an infinitesimal with a real number is infinitesimal, it follows that if , then 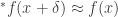, which is the nonstandard analysis criterion for continuity of the function at the real number .

Model Answer 2 (using primarily symbolic logic notation):

Model Answer 3 (using primarily symbolic logic notation):

Model Answer 4 (using primarily symbolic logic notation):

Technically, Model Answer 3 is somewhat better than Model Answer 2, since it shows that the student is aware that one is proving a theorem from a set of assumptions, and the single turnstyle (the symbol 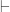) means, to a mathematical logician, that there is a proof from the assumptions on its left side, of the claim symbolized on its right side. However, Model Answer 4 is even a little better than Model Answer 3, because it demonstrates that the student is aware that the kinds of proofs Mathematicians do are semantic in nature, rather than syntactic. Specifically, the double turnstyle, , means to a mathematical logician that all models of analysis satisfying the assumptions on the left of the symbol must also satisfy the claim written on its right. All in all, Model Answer 1, while longer than any of the other three, may be considered a little better, merely because it also reminds the reader of the intuitively obvious (and easily provable) nonstandard analysis fact that the product of a number of “finite magnitude” with an infinitesimal, is always infinitesimal. But what examiner, upon seeing that a student understands the proper notation and usage of Mathematical Logic and its application to real analysis in the form of nonstandard models of analysis, by writing any of these four model answers or something reasonably close to one of them, is going to mark down such a student? Hopefully, no such examiner exists!

In all of these model answers, however, there is some work left to the reader, aka the examiner, because many of the axioms of (standard or nonstandard) analysis are not listed (in Model Answers 2, 3, or 4) to the left of the implication symbol or turnstyle, or included (in Model Answer 1) in the first sentence of the passage given as the answer. But note that in the model answers given by Professor Gower, many axioms of analysis are also not listed, as they are “presumed known” to both the examiner and the examinee. In a sense, this just means that the examiner is not requiring the test-taker to give a perfect, complete, completely rigorous, formal proof. There is then no reason not to accept these shorter nonstandard answers, which are no less rigorous and are no less complete than the standard ones that are typically accepted for full credit.

WordPress Technical Issue: Starting off a bit confused, befuddled, and frustrated

I hate to start off my blog this way, but… somebody must kick off the discussions that improve things for everybody else.

I recently read a post on Tim Gowers’ weblog. I wanted to respond. While my response was brief, it involved some LaTeX code. I was using my iPhone to enter it. Normally I would prefer to use a desktop or laptop, but my iPhone was more convenient this time, except…
After typing in my response to Gowers, I clicked “submit”, and was informed that I am not authorized to post comments to that blog. In fact it seems I must seek permission of some “administrator”. Perhaps that’s Tim Gowers himself? I do not know. But much much more significant is the following fact: the WordPress web site seems to have gobbled up my post and spit it into the ether. I cannot retrieve it and save it for posting after I gain permission from the (unnamed) “administrator”, because in trying to prevent unwanted postings by unauthorized bloggers or blog-bots, this system also prevents valid posts by authorizable bloggers from ever being posted, unless the authorizable blogger in question is already aware that they should not type their response directly into the comments window in WordPress…

My comment, which I attempted to post to Gowers’ blog, amounts to an explanation of how a student can save time on the Cambridge Tripos by giving a nonstandard answer to the problem of showing that differentiability implies continuity, including two model answers. I will not bore you with the details in this post. That will be in a later post, which I shall then copy and paste into the comments section – or there merely reference by providing a link to mine, this new weblog – of Gowers’ posted model answers for Cambridge Tripos problems. Oh yes. I also will not use an iPhone again to post to a blog!